This question was recently brought into focus by the publication of a paper speculating that India’s Covid-19 epidemic would end in September. While this outcome seems highly unlikely, the question of how and when India’s Covid-19 epidemic might end is a valid one.
The good news is that elimination can occur. New Zealand appears to have achieved elimination and other countries, such as Vietnam, South Korea and Australia may soon follow suit. But in many countries, including India, Covid-19 seems to be the unwanted guest who just will not leave.
The goal here is to try, with the help of modelling, to unpack the processes by which Covid-19 epidemics can be controlled – even ended. First, it is helpful to think about what Covid-19 epidemics do not do, and that is best summarised in pictures we see often which look something like this.
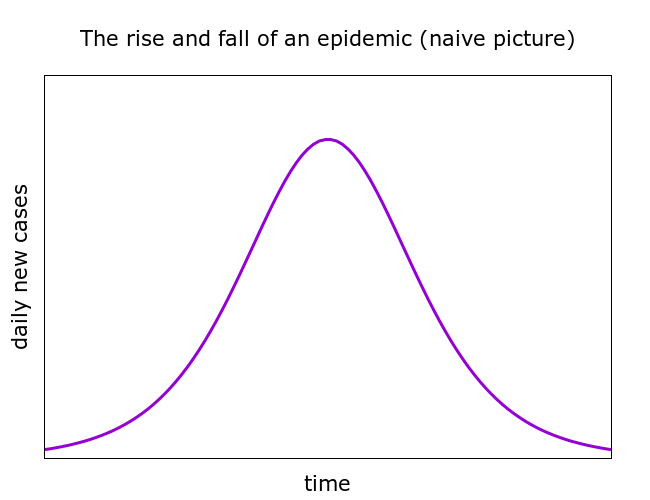
The symmetric rise and fall of an epidemic in such pictures is encoded in an empirical principle known as “Farr’s law”, postulated after studying data from smallpox outbreaks. But real Covid-19 data stands in sharp contrast to the neat symmetry of Farr’s law. Whether countries have been fairly successful in controlling their outbreaks (for example Germany and Denmark), or less so (for example the UK and the US), we generally see a rapid rise and relatively slow and uncertain decline in the daily case numbers.
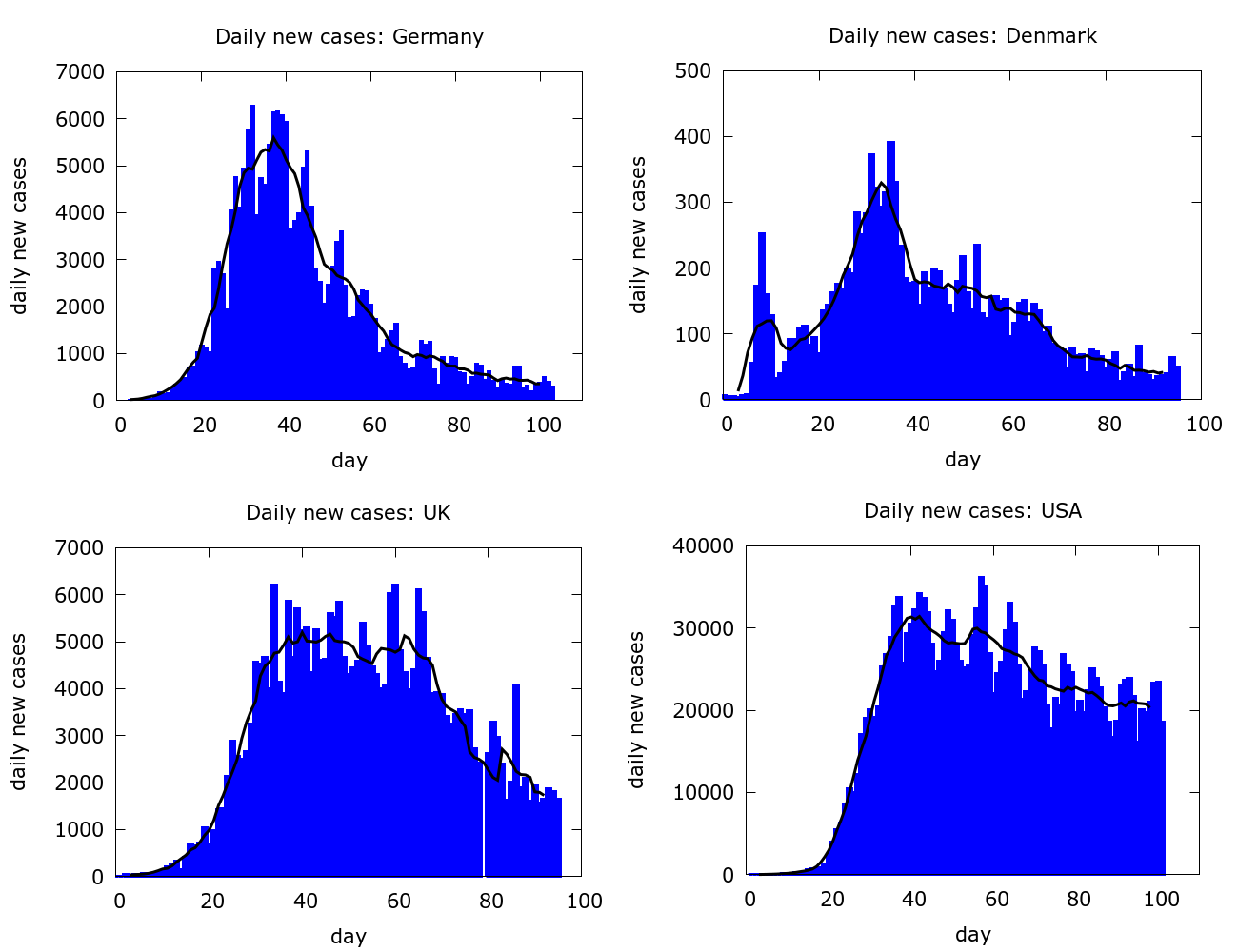
In fact, it is often unclear whether the numbers will tail off towards zero (as in New Zealand), will surge back up (as in Iran), or will simply hover around some baseline level.
So why the discrepancy between the real-world asymmetry and the textbook curve? We find some answers by modelling first very simple scenarios, and then more realistic scenarios, for how an outbreak can wind down. Full details of all simulations are given here.
Underlying the modelling is the following assumption.
Immunity assumption: Most people who get infected with Covid-19 and recover are then immune for a significant period of time (i.e., longer than the time-scale of our modelling).
Although this assumption is not uncontroversial, the evidence so far points to it being broadly correct. Nevertheless, we should remember that we know quite little about the likelihood or duration of post-infection immunity to Covid-19.
Simple scenarios
Simple scenario 1. An outbreak can end because herd immunity develops.
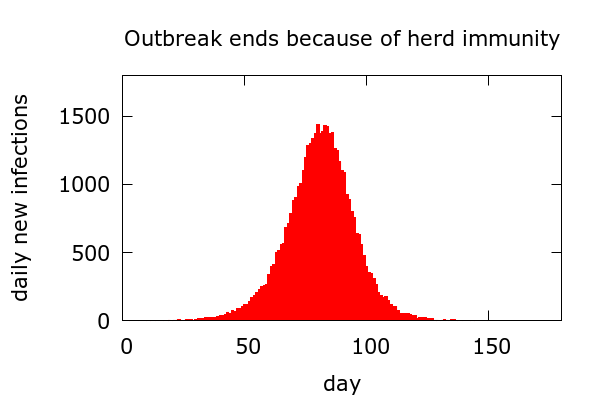
In this scenario, disease sweeps through the population, slowing as more and more infected people recover and acquire immunity. The duration of the outbreak depends on the size of the population, and daily new cases eventually tail off to zero. We see the symmetric rise and fall reminiscent of Farr’s law and can surmise that some process like this was behind the data which led Farr to his law. At the end of the outbreak, the proportion who have been infected depends on the basic reproduction number – the so-called “R0 value” – of the epidemic. Simulations suggest it would not be much below 80% for Covid-19, a devastatingly high figure.
Simple scenario 2. An outbreak can end via the introduction of strong “physical distancing”. This should be read to include increased hygiene, mask wearing, avoidance of gatherings, and all behaviours that reduce infection spreading.
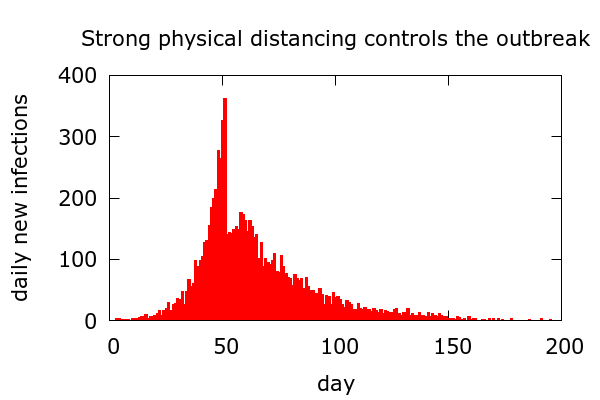
In this simulation, physical distancing begins suddenly, and is strong enough to reduce R below 1. Daily new infections drop immediately and eventually tail off. In real data, we should, within a couple of weeks, see a clear drop in daily cases. With plausible levels of physical distancing, infections tail off more slowly than they rise, and Farr’s law is violated. A noteworthy feature of this scenario is that if mitigation occurs early enough in an outbreak, then only a small proportion of the total population will end up being infected.
More realistic scenarios
Neither simple scenario is able to explain the evolution of Covid-19 outbreaks in general. Firstly, seroprevalence studies have shown that Covid-19 outbreaks – even bad ones as in New York City and London – have not resulted in sufficient immunity to explain the drop-off in infections. Secondly, the data tells us that physical distancing after mitigation is, in general, insufficient to bring R immediately below 1.
Nevertheless, both physical distancing and herd immunity are key to controlling Covid-19. Following lockdown, physical distancing slows transmission; but most importantly lockdown localises disease. To put the latter effect in a simple-minded, but conceptually useful, way: lockdown divides people into those who belong to a community – a household, a close social network, a care home – where there is infection, and those who do not.
Within the “infectible” population, herd immunity develops until eventually infections subside; everyone else is out of view of the virus. Unsurprisingly – as the UK Covid-19 trajectory highlights – the later mitigation begins, the larger the infectible population and the more severe the eventual outbreak.
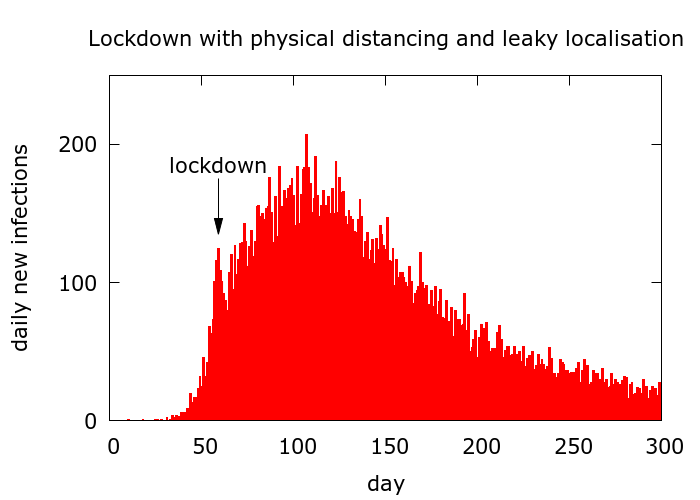
But there’s more to this story: realistically, there will always be leakage into the infectible population, even during the strictest of lockdowns. All it takes for a community to become vulnerable to infection is for one member to be infected. So, there’s a competition between developing herd immunity in the infectible population on the one hand, and the recruitment of new susceptible individuals into this population on the other.
It is the balance between these competing effects that lead to stabilisation of disease levels. The next figure shows a scenario in which lockdown slows transmission and localises the disease. There is, however, leak into the infectible population. Disease levels fall slowly (Farr’s law is violated again) with R values eventually hovering around 1.
Modelling India’s data
India’s Covid-19 epidemic has been slowed but not contained by the lockdown, which failed to prevent severe urban outbreaks. With the lockdown easing, the likelihood of disease being exported from hotspots to new areas – leading to leak, in our framework – is increased. Modelling gives many plausible futures for the outbreak, consistent with its evolution so far.
The next figure shows a simulation whose outputs reasonably match Indian recorded infections to date. This is by no means a “prediction” – simply a simulation consistent with available data, partly to highlight that there is no compelling reason to believe the outbreak will be over by September.
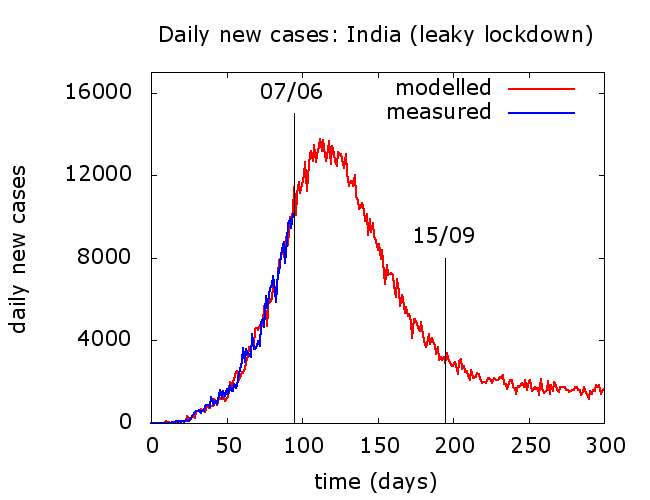
This is quite an optimistic scenario: peak in daily reported cases is reached a few weeks from now and there is no subsequent resurgence. Daily cases decline somewhat slower than they rose and eventually plateau. Different choices of model parameters, all consistent with the data to date, change the height and timing of peak, the speed of descent, and the level of the subsequent plateau.
A long, hard slog
So, Covid-19 outbreaks do not just end. Stringent and effective measures can reduce transmission and localise disease to the extent that – in the best-case – transmission can then be brought effectively to zero through rigorous testing, tracing and isolation.
While this might be the gold standard, the more common reality will likely be that infection is beaten back to relatively low levels, but persists there for months, with occasional new surges until, hopefully, a vaccine is found. The “relatively low levels” will vary widely between different countries/states/cities. Caution and some level of acquired immunity will slow new outbreaks, giving testing, tracing and isolation a better chance of working.
Perhaps most important of all will be surveillance to identify developing hotspots, followed by well-rehearsed containment measures to stop the export of disease to new areas. In a large country like India, elimination may be achieved locally; but in every area one should always expect some spread under the radar and new introductions.
Basically, dealing with Covid-19 is going to be a long, hard, slog. But badly hit countries like the UK, the USA, and Brazil, provide a warning that, despite the difficulties, bringing infection to low levels and maintaining it there must be a priority. The toll from high levels of infection should not be measured only in Covid-19 fatalities, but also in the widespread loss of access to healthcare, the long-term health complications that can follow Covid-19 infection, the disruption to economic and social activity, and the diminishing of life that accompanies widespread fear and uncertainty.
Murad Banaji is a mathematician with an interest in disease modelling. A version of this piece with further details of the modelling and simulations is here.